1. INTRODUCTION

Additive technology is one of the elements of Industry 4.0 [1]. Industry 4.0 also includes the process of testing technological and functional prototypes using 3D printing [1]. The testing of prototypes helps speed up the process of preparing the technological process for mass production [1]. In turn, testing of functional prototypes with properties similar to those of finished products enables a rapid and almost simultaneous refinement of the product at the prototype stage [1,2]. Testing involves, among other things, geometric analysis of the object through, for example, 3D scanning, and testing the mechanical properties (including rheological properties) of the functional prototype [3,4].

Studying the rheological properties of 3D printed parts is very important, if only because these parts can be subjected to longterm deformation or stress [5]. In the case of parts subjected to long-term deformation, one can speak of the phenomenon of stress relaxation [5,6]. Stress relaxation can be described using Maxwell’s model as presented in several articles [7–14]. Maxwell models have different forms: simple and complex models, for example, models based on Prony series or models described by fractional calculus [13,14]. The stress relaxation of additively manufactured parts can vary depending on the print material used or the technological parameters of 3D printing, as confirmed in the articles [15,16].

In the article [7], the author conducted a study of stress relaxation of samples made by selective powder sintering (SLS) technology from PA 2200 material. Samples were produced setting values for two technological parameters: layer height (0.1 mm – 0.4 mm) and print orientation (0°, 90°). Stress relaxation was determined during uniaxial compression testing. The Maxwell-Wiechert model was used to describe the stress relaxation curves. The results showed a clear influence of layer height on stress relaxation. Additionally, it was shown that the orientation of the print affects stress relaxation.

In [17], the authors conducted stress relaxation tests on PLA material using fused deposition technology (FDM). The samples were produced using two technological parameters of the print: the orientation of the print (0°,45°, 90°) and the presence of a contour. In addition, the samples were subjected to different values of deformation and exposure to different temperatures during the tensile stress relaxation tests. To describe the stress-relaxation curves, 3 models were used: Maxwell, Findley and Linear solid. The results showed that Findley's law was the most appropriate empirical expression to predict the PLA tested. Stress distributions ranging from 11% to 14% were obtained. Both cooled and heated samples provided degradation of the quasistatic and long-term material properties. The presented results show the importance of stress relaxation effects in AM PLA structures.

In the article [11], the authors investigated, among other things, the stress relaxations of samples made of G6-Impact nanocomposite using MEX material extrusion technology. The samples were made using the parameter of variable printing direction (0/45/-45/90/90/-45/45/0). The following were carried out: tensile stress relaxations, bending stress relaxations and compressive stress relaxations. On the basis of the results, it was found that the bending mode had the lowest relaxation, while the highest relaxation was observed for the tensile mode.

The viscoelastic behaviour of the materials strongly influences their application area [18,19]. The literature review presented above shows that the viscoelastic behaviour of 3D printed polymers depends on factors such as material type, 3D printing process, and type of load [2,10,20,21]. However, due to the limited number of studies in the field of stress relaxation of 3D printed materials, there is a need for continuous expansion to better understand this phenomenon.

Consequently, the purpose of the article was to determine the elastic moduli and dynamic viscosity coefficients of the PA 2200 polymer material. This material is well suited for medical devices such as orthoses or biomodels. The calculations used the five-parameter Maxwell-Wiechert model to determine the stress relaxation in the material. This research is very important because the calculated coefficients and modulus can be used in engineering calculations.

2. MATERIAL AND METHODS

SLS technology

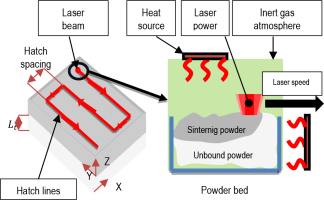
In the presented research, the well-known Formiga P100 machine (EOS GmbH, Krailling, Germany), which realises selective laser sintering - SLS technology, was used to build models. This machine makes it possible to produce physical plastic-based models with dimensions that do not exceed the dimensions of the working chamber of 250 mm × 200 mm × 330 mm. In the mentioned technology, a CO₂ laser is very often used to sinter the input material in the form of powder. The entire technological process is performed in an inert gas. The production scheme using SLS technology is shown in Figure 1 [2,24,25].

Fig. 1.

Principle of SLS technology [2]

Fig. 1 also provides an explanation of the technological parameters in SLS technology such as layer thickness L_t, hatch spacing, laserpower and laser speed.

Samples Preparation

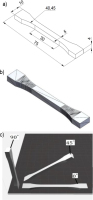
The test samples were designed in SolidWorks according to ISO 527. The shape of the samples are paddles with the dimensions in millimeters shown in Figure 2(a).

Fig. 2.

Test specimens: a) dimensions, b) STL saving, c) print orientation

The STL files of the samples were saved with the following approximation parameters: linear tolerance of 0.007 mm and angular tolerance of 5°. The appearance of the sample in the STL record is shown in Figure 2(b). Six types of samples were produced with different 3D printing technological parameters, each variant was parted 10 times to account for statistical calculations.

The analysed technological parameters of 3D printing were energy density E_d, print orientation P_d and layer height L_t whose values are shown in Table 2. Interpretations of the positioning of the samples on the work platform are shown in Figure 2(c).

Tab. 2.

Values of technological parameters

Ed		Pd	Lt
0.056 J/mm2	0.076 J/mm2	0°, 45°, 90°	0.1 mm
P = 21 W	P=22 W
v = 2500 mm/s	v = 1970 mm/s

The energy density E_d transferred to the sintered layer was calculated using Equation 1 [5,24]:

1

Ed=Pvhχ

where: – laser power, W;v – laser beam speed, mm/s.; h = 0.25 mm (distance between successive laser beams); d = 0.42 mm (diameter of focused beam); x = 1.68 (overlap factor).

Each individual sample was labelled according to the formula: Ed56−Pd0−1, which means Ed56 – energy density, Pd0 – print orientations, 1 – sample number.

The Maxwell-Wiechert model

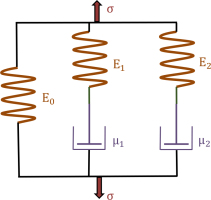
A complex five-parameter Maxwell-Wiechert model was used to describe the stress relaxation curves obtained from the stress relaxation tests. Approximations of this model to experimental curves were carried out with the OriginPro software using the Levenberg-Marquardt algorithm. The mechanical analogy of the Maxwell-Wiechert five-parameter model is shown in Figure 3 [5,13].

Fig. 3.

Mechanical analogy of the Maxwell-Wiechert model [5,13]

The equation describing the Maxwell-Wiechert model consisting of five parameters is as follows [5,13]:

2

σ(t)=σ0+σ1e−tt1+σ2e−tt2

where t₁, t₂ are there relaxation times (s) of each model:

3

t1=μ1E1,t2=μ2E2

After transforming equations (2) and (3), an equation was obtained describing the five-parameter Maxwell-Wiechert model, including all the parameters of this model [5,13].

4

σ(t)=ε0(E0+E1e−E1tμ1+E2e−E2tμ2)

where: ε₀ – unit initial strain; E₀, E₁, E₂ – moduli of elasticity, MPa; μ₁, μ₂ – coefficients of dynamic viscosity, MPa; t – time, s.

The equivalent modulus was also calculated using the following formula [5,13]:

5

Es=E0+E1+E2

where: E₀, E₁, E₂ – moduli of elasticity, MPa.

The decrease in stress after time t was calculated using the formula [5,13]:

6

Rσ=σ0−σtσ0· 100%

where: σ₀ – initial stress, MPa; σ_t – stress after time t, MPa.

Measurement technologies

Stress relaxation tests were conducted using a Hegewald & Peschke Inspekt 3kN testing machine. The test parameters used to conduct the stress relaxation tests were: preload F_p = 100 N, speed of displacement of the machine crossbar to achieve the set strain v_mm = 10 mm/s, permanent strain ε₀ = 0.02, test duration t = 600 s. The test specimens were subjected to tensile stress, as can be seen in Figure 4.

Fig. 4.

Appearance of samples during stress relaxation tests

The test samples were exposed to tensile stresses.

3. RESULTS

Stress relaxation tests were performed, resulting in stress relaxation curves. These curves are shown in Figures 5 and 6.

Fig. 5.

Stress relaxation curves for PA2200 material; Ed56: a) Ed56−Pd0, b) Ed56−Pd45, c) Ed56−Pd90

Fig. 6.

Stress relaxation curves for PA2200 material: d)Ed76−Pd0, e)Ed76−Pd45, f)Ed76−Pd90

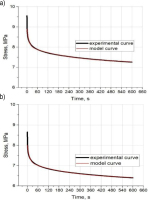
For each individual curve, a five-parameter Maxwell-Wiechert model was approximated using the Levenberg-Marquardt algorithm. An example of the appearance of these fits for selected relaxation curves is shown in Figure 7.

Fig. 7.

Example of a Maxwell-Wiechert model fit to experimental curves: a) Ed56−Pd0−1, b) Ed76−Pd0−1

As a result of fitting of the five-parameter Maxwell-Wiechert model with five parameters to the stress relaxation curves, the values of model parameters σ₀, σ₁, σ₂, σ₁, σ₂ and fitting coefficients Chi², R² were obtained. The values of these parameters and welding coefficients were separated into two tables 3, 4 due to the energy density of the technological 3D printing parameter energy density occurring in two values E_d = 0.056 J/mm² and E_d = 0.076 J/mm².

Based on Table 3, high standard deviation values of standard deviations can be seen for t₂ relaxation times. Low standard deviation values were obtained for the other parameters of the Max-well-Wiechert model and the fit coefficients Chi², R².

Analysing the data collected in Table 4, high values of standard deviations can be observed for the t₂ relaxation times. Low standard deviation values were obtained for the other parameters of the Maxwell-Wiechert model and fit coefficients Chi², R².

Based on the average values of the Maxwell-Wiechert model parameters σ¯0, σ¯1, σ¯2, t¯1, t¯2 and the values of the constant strain ε₀ = 1 mm, using formulas (2), (3) and (4), the elastic moduli E₀, E₁, E₂ and the dynamic viscosity coefficients μ₁, μ₂ were calculated. The values of these moduli and coefficients are shown in Figures 8, 9. Furthermore, using formula (5), the equivalent modulus E_s was calculated, which is also shown in Figure 8.

Fig. 8.

Moduli of elasticity for PA 2200 material

Fig. 9.

Dynamic viscosity coefficients for PA 2200 material

The stress relaxation curves obtained from the tests were used to calculate, according to Equation (6), the percentage decrease in stress R_σ after time t. The values of the percentage decrease in R_σ stress are shown in Table 5.

In the data in the table above, it is evident that the highest decrease in stress occurred for Ed56 and Pd45. While the lowest decrease in stress was for Ed56 and Pd0.

In the data in the table above, it is evident that the highest decrease in stress occurred for Ed56 and Pd45. While the lowest decrease in stress was for Ed56 and Pd0.

4. DISCUSSION

The translation of stress relaxation curves seen in Figures 5 and 6, and particularly noticeable for samples printed according to technological parameters Ed56−Pd45 may be due to the difficulty of realising a unit stress stroke. The unit stress stroke is performed at the highest possible speed, which is difficult to perform under laboratory conditions. Also, the difficulty of setting a pre-stress for each individual specimen, can cause an apparent translation of test results. Too high values of pre-stress will cause the specimen to begin relaxing stresses even before the test begins, while too low values will lead to a stress stroke that is not correct to achieve the set strain.

Based on Figure 7, the Maxwell-Wiechert fit of the five-parameter model to the stress relaxation curves is strong. This can be concluded not only from a visual assessment of Figure 7 (the red line overlaps with the black line), but also by turning our attention to the values of the Chi² fit test coefficients and R² determination coefficients shown in Tables 3 and 4. It should be mentioned here that the R² determination coefficient always varies between ‘0’ and “1” and is a measure of the fit of the regression equation R² values close to “1”, i.e. those shown in Tables 3 and 4, indicate that the regression equation is very useful to predict the value of the dependent variable Y with the independent variable X. For the Chi² concordance test, values close to ‘0’ indicate a strong model fit.

The high standard deviation values for the stress relaxation time t₂(Table 3 and 4) may be related to dynamic viscosity. The dynamic viscosity, on the other hand, depends on the structure at the molecular level of the material in this case PA 2200, which is a polymer. Polymers are made up of long polymer chains that form numerous intermolecular interactions.

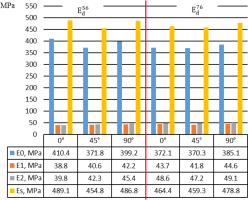
When analysing the data in Figures 8 and 9, that is, the elastic moduli E₀, E₁, E₂and the dynamic viscosity coefficients μ₁, μ₂, one can see a slight anisotropy of the stress relaxation properties due to the orientations of the print.

Analysing the elastic moduli E₀, E₁, E₂ p shown in Figure 8, it can be concluded that, there are differences within the same direction, e.g. the modulus of E₀ is many times greater than the moduli of E₁, E₂. This regularity informs that in terms of viscoelastic properties the material produced by selective laser sintering technology can be quasi-isotropic.

Analysing the different print orientations 0°, 45°, 90° for the equivalent moduli E_s and dynamic viscosity coefficients μ₁, μ₂ shown in Figures 8 and 9, it can be seen that there is a difference in values between the applied energy densities E_d = 0.056 J/mm² and E_d = 0.076 J/mm². The equivalent moduli of E_s for print orientations 0°, 90° and energy density Ed56 are 5% and 2% larger, respectively, than the same equivalent moduli and print orientation, but for energy density Ed76. The value of the equivalent modulus E_s with print orientation 45° and Ed56 was 1% smaller than the same modulus for the same print orientation but energy density Ed76. For dynamic viscosity coefficient μ₁ the differences between the energy densities for print orientations 0°, 45°, 90° were 20%, 6%, 7%, respectively, in favor of energy density μ or dynamic viscosity coefficient 0°, 45°, 90° the differences between energy densities for print orientations Ed76.

However, for energy density Ed76 and print orientations 0°, 90° the values of percentage stress drop values are higher by 14%, 6%, respectively, compared to the same orientations but for lower energy density Ed56. In contrast, for print orientation 45°, the value of percentage stress drop for energy density Ed56 was 1% higher than the same value but for energy density Ed76.

5. CONCLUSSIONS

On the basis of the results of the stress relaxation tests, the following general conclusions can be drawn:

The calculated values of the elastic moduli E₀, E₁, E₂ and dynamic viscosity coefficients μ₁, μ₂ can be used to model components produced by selective powder sintering (SLS) technology from PA2200 material. In particular, the application of these moduli and dynamic viscosity coefficients can be found in engineering calculations.