INTRODUCTION
In recent years, the mixed convection of magnetic nanofluids in various geometries has garnered increasing attention. Several studies have highlighted the diverse applications of this innovative class of nanofluids, including the works of Nandy and Yanuar [1], Sohel et al. [2], and Heris et al. [3]. Ahmed et al. [4] investigated the mixed convection of micropolar nanoliquids in a double lid-driven cavity. They reported an increase in the Nusselt number (Num) as the volume fraction (ϕ) increases, while it decreases as the length of the heat source increases.
Teamah et al. [5] investigated mixed convection in a square cavity filled with nanofluids. They observed that the mean Nusselt number (Num) increases with Reynolds (Re) and Rayleigh (Ra) numbers, but decreases as the volume fraction (ϕ) increases. In another innovative study, Garoosi et al. [6] numerically examined the mixed convection of nanoliquids. The effects of Re and Ra on heat transfer, fluid movement, and entropy generation in a nanoliquid-filled square cavity were studied by Mirmasoumi and Behzadmehr [7]. They found that Num increases with Re, Ra, and ϕ. Raisi et al. [8] studied the heat transfer by mixed convection of a Cu-water nanofluid in a vertical parallel plate channel. They found that an increase in the solid volume fraction leads to an enhancement in the heat transfer rate, particularly at low Richardson numbers. A numerical simulation of mixed convection in inclined horizontal tubes with a uniform heat flux, using a nanofluid, was conducted by Akbari et al. [9]. The results showed that the Al2O3 concentration had no significant effect on the hydrodynamic parameters, and the heat transfer coefficient was maximal when the inclination angle was 45°.
In the presence of magnetic field effects, a numerical study on mixed convection in different geometries was conducted by Ali et al. [10, 11]. They suggest that the heat transfer rate depends on various physical parameters and geometric configurations. Furthermore, the heat transfer rate decreases with an increase in the magnetic field intensity. In another study, Kefayati [12] conducted a numerical examination of magnetic mixed convection. The analysis indicates that heat transfer decreases as the Hartmann number (Ha) increases. Akram et al. [13] studied MHD mixed convection in a chamfered square enclosure filled with water, analyzing the impact of magnetic field orientation on flow and heat transfer. Their results showed that both the intensity of the magnetic field and the inclination angle significantly influence heat transfer, with Nusselt numbers generally decreasing as the Hartmann number increases. Maya et al. [14] examined a lid-driven cavity with a rectangular heat source under the influence of a magnetic field, highlighting the importance of the Hartmann number in altering flow patterns and heat transfer rates.
Additionally, Mliki et al. [15, 16] studied mixed convection under the influence of the Lorentz force. They observed that in the presence of a magnetic field, the average Nusselt number along the hot wall shows a significant dependence on several parameters. Specifically, this number increases with the Reynolds number (Re), which is generally associated with higher fluid velocity and flow intensity. On the other hand, the Nusselt number decreases with an increase in the Hartmann number (Ha). These results underscore the complex effect of the magnetic field on the mixed convection process and highlight the need to consider the interaction between these different parameters for more accurate modeling of thermal phenomena in conducting fluids. Also, Mliki et al. [17, 19] used LBM to examine the effect of nanoparticles Brownian motion on fluid movement in different geometries. Prosenjit al. [20] used a commercial finite element solver “COM-SOL Multiphysics 6.0 to examine the MHD mixed convection in a semicircular cavity with hybrid nanofluids. They found that the heat transfer increases with an increase in Ri but decreases with the rise of the Hartmann number (Ha). In another innovative study, Falah et al. [21] investigated the mixed convection phenomenon of a hybrid nanofluid flowing within a horizontally oriented channel, featuring a triangular cavity attached to the lower channel wall. They found that the average Nusselt number increases with higher Reynolds number, angular rotation speed, cylinder position, and Richardson number.
Mliki et al. [22] investigated the influence of a horizontal periodic magnetic field within a double-lid U-shaped enclosure. By comparing scenarios that included and excluded the effect of Brownian motion, they demonstrated that Brownian motion significantly enhances heat transfer under all defined conditions. In a related context, Ighris et al. [23, 24] explored the application of the Lattice Boltzmann Method (LBM) to model natural convection in hybrid nanofluids. Their work emphasized the advantages of this approach, particularly in terms of numerical stability and accuracy. Additionally, Hadoui et al. [30] studied natural double-diffusive convection in a square cavity filled with an Al2O3-water-based nanofluid. Their findings revealed that the heat transfer rate increased with the nanoparticle volume fraction, while the mass transfer rate decreased. Recently, Thilagavathi et al. [25] conducted a study on heat transfer enhancement in a magnetic ternary hybrid nanofluid within a hexagonal cavity containing a square obstacle. The findings of this research demonstrate that the appropriate incorporation of nanoparticles significantly enhances the heat transfer properties of base fluids.
In recent years, magnetohydrodynamic (MHD) mixed convection of nanofluids in porous systems has attracted considerable attention due to its industrial and energy-related applications. For instance, Mandal et al. [26] investigated the MHD mixed convection of a hybrid nanofluid in a W-shaped porous system, emphasizing the influence of geometry and nanofluid properties on thermal and hydrodynamic transfer processes. Their findings demonstrated that thermal energy transfer significantly depends on the length of the heating and cooling surfaces, the fluid volume within the cavity, and the amplitude of the bottom undulation height in the W-shaped cavity. Additionally, Mandal et al. [27] examined the role of surface undulations during mixed bioconvective flow of a nanofluid in the presence of oxytactic bacteria and magnetic fields. Their study revealed that the complex interactions between magnetic forces, bioconvection, and the properties of the porous medium play a critical role in enhancing heat and mass transfer. In addition, Alomari et al. [28] performed a numerical analysis to examine the effect of a porous block on MHD mixed convection in a split lid-driven cavity containing a nanofluid. Their study demonstrated the significant impact of the porous block on thermal and hydrodynamic performance, particularly in complex configurations such as split lid-driven cavities.
This study distinguishes itself through its innovative numerical analysis of mixed convection in a nanoliquid (CuO/water) within a double-lid driven convergent cavity featuring discrete heating, under the influence of a horizontal magnetic field. Unlike previous studies, this research simultaneously investigates the combined effects of convergent cavity geometry, discrete heating, and a horizontal magnetic field on the thermal and dynamic characteristics of the flow.
PROBLEM DEFINITION
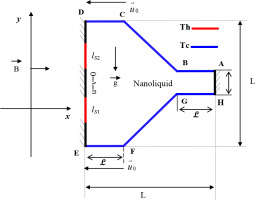
We consider the magnetic nanoliquid mixed convection in a heated thermal convergent cavity. The configuration of the physical model is shown in Fig. 1. Two heat sources are situated at the left wall at constant temperature. The aspect ratio of the enclosure is defined as AR = L/L=0.3. As visible from the graphical view, the superior and bottom walls of the cavity are cold and moving with a constant velocity
MATHEMATICAL FORMULATION
To investigate the mixed convection flow, certain assumptions are made to simplify the analysis.
Key Assumptions in the Study
Steady-State Flow: The study assumes that the flow is steady, meaning that the fluid properties (velocity, pressure, temperature, etc.) do not change with time.
Incompressible Flow: The fluid is assumed to be incompressible, implying that the density remains constant throughout the flow field. This assumption is valid for liquids and for gases at low Mach numbers (typically < 0.3).
Laminar Flow: The flow is assumed to be laminar, meaning that the fluid moves in smooth layers or streams without significant mixing. This assumption is reasonable for flows with low Reynolds numbers.
Negligible viscous dissipation: The study assumes that the energy generated by viscous dissipation is negligible. This means that the heat produced by internal friction within the fluid is insignificant compared to the other energy terms in the system.
Negligible Heat Generation: The study assumes that there is no significant heat generation within the fluid, either from chemical reactions, electrical heating, or other sources. This simplifies the energy equation by removing the heat generation term.
Constant Fluid Properties: The fluid properties such as viscosity, thermal conductivity, and specific heat are assumed to be constant. This assumption is valid for small temperature variations within the flow.
No Radiation Heat Transfer: The study assumes that heat transfer due to radiation is negligible compared to conduction and convection. This is reasonable for many engineering applications where temperatures are not extremely high.
Governing equations
By applying the Boussinesq approximation, the governing equations for this investigation are as follows [29]:
For this problem, the fluid flow is subjected to gravitational force:
In addition to the gravitational force, the flow of the nanohybrid is subjected to the volumetric Laplace force:
To calculate this volumetric Laplace force, it is more appropriate to use the dimensionless Hartmann number, defined by:
This number is used in fluid dynamics, particularly in the study of conducting fluids in the presence of a magnetic field. It characterizes the influence of magnetic forces in relation to viscous forces within a fluid.
Where σnf is the electrical conductivity, B is the magnetic field intensity, L is the characteristic length of the cavity, and μnf is the dynamic viscosity of the nanofluid.
For Magneto-Hydro-Dynamic (MHD) nanoliquid mixed convection flow, the expression for local entropy generation, Sgen, can be formulated as follows [30]:
The effective density, heat capacitance, thermal expansion coefficient, thermal diffusivity, and electrical conductivity of the nanoliquid are defined as follows [31]:
The thermal conductivity of the nanoliquid is determined using the following equation [32]:
The effective dynamic viscosity of the nanofluid is determined using the Brinkman model [33]:
A numerical investigation of mixed convection was carried out using the following dimensionless variables:
16
The Reynolds number (Re) is one of the most important dimensionless parameters in fluid mechanics. It is used to characterize the flow regime of a fluid, whether it is laminar, transitional, or turbulent. It is defined as the ratio of inertial forces to viscous forces in a fluid flow.
By introducing the dimensionless variables mentioned above, the governing equations (1-4) are transformed into their non-dimensional forms, which can be expressed as follows:
Dimensionless entropy generation Sgen can be obtained as:
Where X is the irreversibility factor. It is defined by:
The average entropy generation is calculated by:
Where V is the total volume of the physical domain.
The local and average Nusselt numbers along the two heat sources (lS1, lS2) can be calculated using the following expressions:
NUMERICAL METHOD AND VALIDATION
The given equations have been numerically solved using the lattice Boltzmann method (LBM), as detailed in Mliki et al. [31]. This approach was based on Ludwig Boltzmann’s kinetic theory of gases. Employing the Bhatnagar-Gross-Krook approximation, the lattice Boltzmann method involves two distribution functions, denoted as g and f, representing the temperature and the flow field, respectively, Eqs. (26) and (27):
Here, Δt represents the lattice time, and τv and τα denote the lattice relaxation times for the flow and temperature fields, respectively.
Two local equilibrium distribution functions for the temperature and flow fields
The variables u and ρ represent the macroscopic velocity and density, respectively. The lattice speed c is defined as c=Δx/Δt, where Δx is the lattice spacing and Δt is the lattice time step, both of which are set to unity. Furthermore, ωi denotes the weighting factor for the flow field, while
Consequently, the weighting factors and discrete particle velocity vectors differ between these two models and are calculated using Eqs. (30-33) as follows:
For D2Q9:
The discrete velocities for the D2Q9 (Fig. 2) are defined as follows:
For D2Q4:
The weighting factor for temperature in each direction is:
The discrete velocities for the D2Q4 (Fig. 3) are defined as follows:
The relationship between the kinematic viscosity ν and thermal diffusivity α with the relaxation time is expressed by Eq. (34):
Where cs is the lattice speed of sound, equal to
With Fi is the total external body force.
The macroscopic quantities ρ, u, and T can be calculated by Eq. (36):
SOLUTION METHOD
To ensure the applicability of the code in a nearly incompressible regime, the characteristic velocity must be significantly lower than the speed of sound in the fluid. Therefore, in the simulations, the Mach number is set to less than Ma=0.3. In this study, the Mach number is fixed at Ma=0.1 for all considered cases. Viscosity and thermal diffusivity are determined based on the definitions of the corresponding dimensionless parameters, while maintaining constant values for the Rayleigh number, Prandtl number, and Mach number.
With N indicating the total number of lattices positioned in the y-direction.
The stream function and vorticity are defined as:
where ω and ψ are vorticity and stream function, respectively.MESH VERIFICATION AND VALIDATION
For the grid sensitivity analysis, Tab. 2 presents the results obtained using four different mesh sizes. The simulations revealed that the difference in results between the grid sizes of 100×100 and 150×150 was minimal. Based on these findings, the grid size of 100×100 was selected for the analysis.
Tab 2.
Grid independence test for
| Average Nusselt number | ||
|---|---|---|
| Lattice size | Re=1 | Re=100 |
| 50×50 | 1.7632 | 7.3423 |
| 75×75 | 2.1482 | 8.8753 |
| 100×100 | 2.5483 | 9.6128 |
| 120×120 | 2.5502 (0.07%) | 9.6412 (0.2%) |
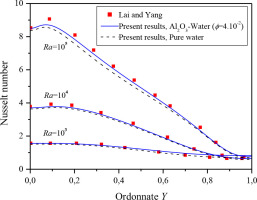
For data validation, the present results are compared with the numerical results from Lai and Yang [34] for the case of nanoliquid natural convection in a square enclosure (Fig. 4).
Fig. 4.
Comparison of the local Nusselt number along the hot wall between the present results and numerical results by Lai and Yang [34]
Additionally, the temperature distribution along the axial midline is compared between the present results and those obtained by Ghassemi et al. [35] for magnetic nanoliquid mixed convection in a square enclosure (Fig. 5). Another validation test is performed for the case of mixed convection (Fig. 6), where the current numerical results are compared with the results from Talebi et al. [36]. Based on these comparisons, the developed code is demonstrated to be reliable for studying MHD mixed convection of a nanoliquid in a double-lid driven thermally convergent cavity.
Fig. 5.
Comparison of the temperature on axial midline between the present results and numerical results by Ghassemi et al. [35] (ϕ =3.10-2, Ra=105)
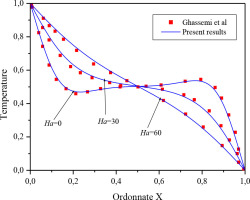
Fig. 6.
a) Horizontal component of velocity b) vertical component of velocity with those of Talebi et al. [36]

RESULTS AND DISCUSSION
A numerical analysis of two-dimensional magnetohydrodynamic (MHD) mixed convection is conducted for a CuO–water nanoliquid within a double lid-driven thermally convergent cavity. The study investigates the fluid flow and heat transfer characteristics under the influence of magnetic fields, focusing on the behavior of the nanoliquid in this specific configuration.
Effects of Reynolds number
The main objective of this numerical study is to evaluate the effects of the Reynolds number (Re) on isotherms, local entropy generation, and streamlines inside the cavity saturated with CuO-water nanofluid, for Ri = 20, ϕ= 4.10-2, and Ha = 0. For Re = 1, the flow, local entropy generation, and temperature contours are nearly symmetric about the horizontal centerline (Y = 0.5) of the cavity and are concentrated along the two heated sources (lS1 and lS2) due to the enhanced fluid movement in these regions. In this case, the flow is characterized by the presence of two symmetric counterclockwise vortices, rotating in opposite directions with intensities (|ψ|max = 7.16 × 10−2 and 6.91 × 10–2), respectively (Fig. 7). As the Reynolds number increases, the influence of the moving walls (CD and EF) becomes increasingly significant, leading to substantial changes in the flow dynamics within the cavity. These walls, moving relative to the fluid, introduce a forced convection component that enhances fluid circulation in the surrounding regions. This effect is especially prominent in the lower part of the cavity, where the largest circulation cell develops.
Fig. 7.
Streamlines, Isotherms and Entropy generation lines for different Re at Ri=20, Ha=0, and ϕ= 4.10-2
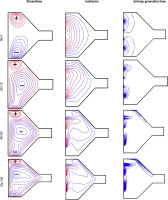
In this figure, at low Reynolds numbers (Re = 1), heat transfer within the cavity is primarily dominated by conduction, with isotherms appearing nearly parallel to the isothermal walls. As the Reynolds number increases (Re = 10, 50, and 100), the cold nanofluid penetrates deeper into the corners (D and E), intensifying the temperature gradients around the discrete heat sources (lS1 and lS2). Additionally, enhanced circulation of the nanofluid is observed on the left side of the cavity (zone ABGH), resulting in a more efficient heat transfer process. The effect of increasing the Reynolds number on entropy generation is also illustrated in Fig.7. It is observed that an increase in the Reynolds number enhances fluid motion, resulting in a higher concentration of entropy generation contours near the discrete heat sources. This leads to the formation of active regions of entropy generation, which are particularly pronounced at higher Reynolds numbers (Re = 10, 50, and 100).
In summary, an increase in the Reynolds number significantly modifies the distribution and intensity of entropy generation within the cavity. These changes are primarily driven by the intensification of forced convection, which enhances temperature and velocity gradients, leading to the formation of active entropy generation zones near the heat sources and in regions of increased fluid circulation. These findings underscore the importance of accounting for the effects of the Reynolds number in the design and optimization of heat transfer systems that utilize nanofluids.
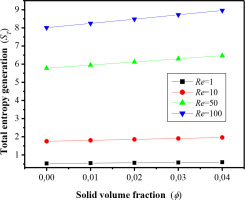
The effect of solid nanoparticle concentration on the Nusselt number (Num) along the discrete heat sources (lS1 and lS2) is illustrated in Fig.8. A detailed analysis of Equation (14) shows that increasing the concentration of solid nanoparticles in the nanofluid directly enhances its effective thermal conductivity. This enhancement is critical, as it improves heat transfer through the fluid, particularly in the regions near the heat sources where the heat transfer intensity is highest. As a result, the fluid becomes more effective in transferring heat, leading to an increase in the Nusselt number. In Fig.9, the total entropy generation (Sgen) exhibits a trend similar to that of the Nusselt number (Num). This correlation can be explained by the fact that the enhancement of heat transfer, driven by the increase in nanoparticle concentration, is accompanied with an increase in thermodynamic irreversibilities, as measured by entropy generation.
Fig. 8.
Average Nusselt number for different values of the Reynolds numbers and volumetric fraction of nanoparticles (ϕ) at Ri=20, Re=100 and Ha=0
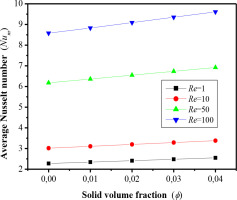
Fig. 9.
Total entropy generation for different values of the Reynolds numbers and volumetric fraction of nanoparticles (ϕ) at Ri=20, Re=100 and Ha=0
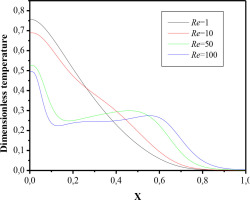
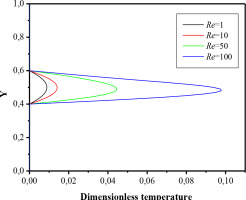
Figs 10 and 11 illustrate the temperature profile within the cavity at two specific positions: x/L = 0.5 and y/L = 0.75, for different Reynolds numbers (Re). These graphs provide a detailed analysis of how temperature evolves within the cavity as Re changes. It is clearly observed that the temperature in the ABGH region of the cavity increases with higher Re. This trend can be attributed to the increasing influence of mixed convection heat transfer, which becomes more dominant as Re rises. At low Reynolds numbers, heat transfer is mainly governed by thermal conduction, a slower and less efficient mechanism for heat transfer. However, as Re increases, mixed convection enhances heat transfer, leading to a more significant temperature rise in regions close to the heated walls of the cavity, particularly in the ABGH area. This behavior underscores the importance of fluid velocity and the convection regime in optimizing heat transfer within confined systems such as the one studied. These findings highlight the critical role of Reynolds number in controlling heat transfer dynamics and suggest that optimizing fluid flow conditions can significantly improve the efficiency and reliability of thermal management systems in practical applications.
Effects of Hartmann number
The effects of the Hartmann number (Ha) on the streamlines and entropy generation contours for Re = 100, Ri = 20, and ϕ = 4.10-2 are shown in Fig.12. The presence of a magnetic field leads to a significant reduction in mixed convection, resulting in an unfavorable impact on heat transfer. While buoyancy enhances heat transfer, the Lorentz force induced by the magnetic field counteracts this effect, reducing thermal transfer efficiency and minimizing entropy generation, making the process less favorable for optimizing heat transfer. As observed, an increase in the Hartmann number results in a reduction in flow intensity, with the minimum value occurring at the highest Hartmann number. The maximum value of the stream function is 3.68 × 10−1 for Ha =0, 2.94 × 10−1 for Ha = 20, and 1.5 × 10−1 for Ha = 80, which explains the stagnation of the stream function at Ha = 80. This flow stagnation at high Hartmann numbers has significant implications for heat transfer dynamics. Specifically, the reduction in mixed convection results in a greater dominance of thermal conduction. As a consequence, while entropy generation is reduced due to the decrease in irreversibilities associated with fluid motion, the overall heat transfer efficiency is diminished.
Fig. 12.
Streamlines, Isotherms and Entropy generation lines for different Ha at Re =100, Ri=20 and ϕ= 4.10-2
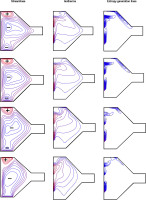
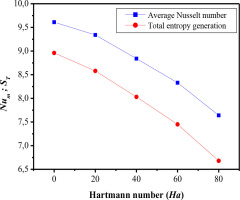
Fig. 13. illustrates the effect of the Lorentz force on the variation of the average Nusselt number and total entropy generation for different Hartmann numbers (Ha = 0, 20, 40, 60 and 80) at a solid particle concentration of ϕ = 0.04. It can generally be observed that the average Nusselt number decreases as the Hartmann number (Ha) increases. This decrease is primarily attributed to the inhibitory effect of the Lorentz force, which opposes fluid motion and reduces the intensity of mixed convection. In the absence of a magnetic field (Ha = 0), the average Nusselt number reaches its maximum value, reflecting optimal mixed convection and efficient heat transfer. However, as Ha increases, the Lorentz force becomes more dominant, slowing down the flow and thereby reducing the contribution of convection to heat transfer. Consequently, heat transfer becomes increasingly dominated by conduction, a less efficient mechanism compared to convection. The variation in entropy generation follows a trend similar to that of the Nusselt number. At low Hartmann numbers (Ha = 0), entropy generation is relatively high due to the irreversibilities associated with intense fluid motion and pronounced temperature gradients. However, as Ha increases, the reduction in flow intensity decreases these irreversibilities, leading to a gradual decline in entropy generation.
Fig. 13.
Effect of Hartmann number on average Nusselt number and on total entropy generation for different Hartmann numbers at Ri = 20, Re= 100 and ϕ= 4.10-2
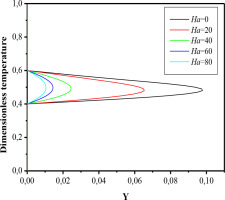
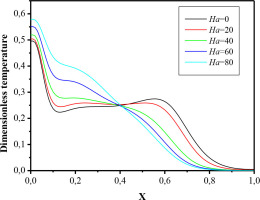
Figs. 14 and 15 show the temperature profile within the cavity at two specific positions: x/L = 0.5 and y/L = 0.75, for different Hartmann numbers (Ha). These graphs provide a detailed analysis of how the temperature evolves within the cavity as Ha changes. It is clearly observed that the temperature in the ABGH region of the cavity decreases as Ha increases. This trend can be attributed to the reduced influence of mixed convection heat transfer, which becomes less significant as Ha increases. At high Hartmann numbers, heat transfer is primarily governed by thermal conduction. This results in a more significant decrease in temperature in the ABGH region.
CONCLUSION
This study introduces an innovative approach to investigate mixed convection heat transfer by analyzing the influence of a magnetic field on heat transfer and flow characteristics in a convergent double-lid-driven cavity with discrete heating. The effects of the Reynolds number (Re), Hartmann number (Ha), and nanoparticle volume fraction (ϕ) on flow dynamics and heat transfer performance were systematically examined. The primary conclusions derived from the numerical results are as follows:
– For all considered values of Re and Ha, increasing the nanoparticle volume fraction leads to an increase in the average Nusselt number and total entropy generation.
– As the Reynolds number (Re) the values of the Nusselt number (Num) also increase.
– The maximum value of the stream function (|ψ|max) is achieved at Re = 100.
– When a magnetic field is applied, the velocity of the nanoliquid decreases, which in turn leads to a reduction in the maximum value of |ψ|max.
– Both the Nusselt number (Num) and entropy generation are inversely related to the Hartmann number (Ha).
– The temperature in convergent cavity increases with an increase in Re, whereas the opposite effect is observed when Ha increases.
– The influence of Ha on Num and entropy generation is more pronounced at higher Reynolds numbers (Re = 50 and 100).
Based on the results presented in this article, it is recommended to use a combination of Re = 100, Ha = 0 (absence of a magnetic field), and ϕ = 0.04 to maximize heat transfer. However, if entropy generation must be minimized, a compromise with Ha = 80 is suggested. This higher Hartmann number value will improve flow control and reduce entropy generation while maintaining acceptable heat transfer performance. This approach is particularly beneficial in applications where energy efficiency and loss minimization are top priorities.